Межрегиональная модель динамического стохастического общего экономического равновесия

Введение

Основная задача Банка России — поддержание ценовой стабильности, т. е. поддержание темпов роста цен вблизи целевой инфляции. Это, в свою очередь, порождает необходимость прогнозирования траектории инфляции на несколько кварталов вперед. Однако при принятии решений в рамках проводимой денежно-кредитной политики (ДКП) необходимо также учитывать региональные особенности и тенденции. Так, например, инфляционные процессы и темпы роста экономики Центрального федерального округа (ЦФО) и Российской Федерации в целом могут значительно отличаться. Это, в свою очередь, порождает необходимость моделирования межрегионального взаимодействия внутри экономики России.

Одним из самых распространенных инструментов анализа протекающих в экономике процессов являются структурные модели. В настоящей работе представлена модель динамического стохастического общего экономического равновесия (ДСОЭР), позволяющая строить прогнозы развития региональной экономики в среднесрочной перспективе и проводить сценарный анализ развития экономических процессов. В данной модели присутствуют два региона: ЦФО и остальная часть России, что позволяет проводить анализ последствий как региональных, так и федеральных шоков.

Теоретический анализ

С. Г. Синельников-Мурылев, Ю. Н. Перевышин и П. В. Трунин [7] выделяют несколько проблем, которые могут возникать из-за различий в уровне инфляции между регионами. Если премии за риск в разных регионах одинаковы, то в регионах с более высокой инфляцией реальные процентные ставки окажутся ниже по сравнению с регио­нами, где инфляция низкая. Это может вызвать различия в динамике инвестиций и потребительского спроса. Кроме того, если в одних регионах цены растут, а в других падают, то регион, столк­нувшийся с дефляцией, рискует оказаться в дефляционной спирали.

При принятии решений в рамках проводимой ДКП важно понимать, временный или постоянный характер имеют различия инфляционных процессов в регионах. Исследователи [9; 10] задаются вопросом устойчивости факторов, влияющих на различия в инфляционных процессах.

Некоторые труды [6; 1] связывают различия в инфляции между регионами с эффектом Балассы — Самуэльсона. Другие исследования [7] утверждают, что различия в динамике инфляции обусловлены влиянием тех или иных факторов в разных регионах. Наконец, ряд авторов [5; 12] подчеркивают влияние отраслевых особенностей на общероссийскую инфляцию, рассматривая их как региональные из-за низкой диверсификации региональной экономики. Отдельно стоит отметить работу [4], в которой региональные особенности инфляции исследуются с помощью региональной Квартальной прогнозной модели (КПМ) экономики ЦФО.

Эмпирический анализ

Модель, представленная в данной работе, построена на основе неоклассических моделей роста и рассматривает малую закрытую экономику. В модели присутствуют следующие основные экономические субъекты: домохозяйства, фирмы, инвестиционные производители, отечественные поставщики, Центральный банк и правительство. При разработке модели использовались стандартные подходы [2; 3; 8; 11; 13]. В качестве отличительной особенности представленной модели можно назвать разделение России на два макрорегиона: ЦФО (Центральный федеральный округ) и ОРР (остальные регионы России). Каждый из макрорегионов моделируется как отдельная малая открытая экономика, взаимодействующая со вторым регионом. Более детальное описание этого подхода дано в работе [8], где авторы представили аналогичную нашей ДСОЭР-модель для еврозоны. В этой модели еврозона разделена на два субрегиона: рассматриваемая страна и остальная часть еврозоны. Эти субрегионы связаны через торговые и финансовые потоки, а также объединены общей монетарной политикой. Схожим образом в нашей модели ЦФО и ОРР взаимодействуют через экономические связи, что позволяет учитывать региональные особенности и их влияние на общую экономическую динамику.

В отличие от работы [8], где регион остальной части еврозоны представлен упрощенно, фактически как внешний сектор, в предлагаемой региональной ДСОЭР-модели оба макрорегиона — ЦФО и остальная часть России — моделируются равноправно и с одинаковой степенью детализации.

Модель состоит из нескольких экономических субъектов ЦФО и ОРР — домохозяйств, фирм, инвестиционных производителей, отечественных поставщиков (ретейлеров), Центрального банка, правительства, — связанных финансовыми и товарными потоками, а также факторами производства.

Макрорегионы взаимодействуют между собой тремя способами:

1. Инвестиционные производители покупают товар у производителей ЦФО и ОРР, объединяют их в единый товар, который преобразуют в капитал согласно уравнению эволюции капитала:

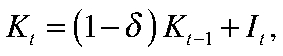
где 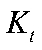 — капитал,  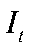— инвестиции.

2. Фирмы берут капитал в аренду у инвестиционных производителей ЦФО и ОРР, объединяют их и используют для производства товаров согласно производственной функции Кобба — Дугласа.

3. Отечественные ретейлеры покупают товары у производителей ЦФО и ОРР, объединяют их и продают домохозяйствам соответствующих регионов.

В модели не предусмотрена миграция трудовых ресурсов между регионами. Для упрощения функция банковской системы передана Центральному банку, который напрямую кредитует домохозяйства. Жесткость цен и зарплат, а также механизм подстройки капитала моделируются в соответствии с подходом Ротемберга [14].

Поскольку блоки ЦФО и ОРР структурно идентичны, уравнения представлены только для блока ЦФО. Переменные ЦФО обозначены индексом 1, а переменные ОРР — индексом 2. В результате решения оптимизационной задачи домохозяйств получаются следующие уравнения.

1. Уравнение Эйлера:

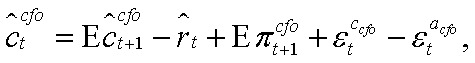
где 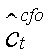 — разрыв потребления ЦФО;  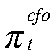— разрыв инфляции ЦФО;  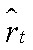— разрыв ставки ЦБ;  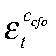— шок спроса ЦФО;  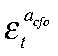— отклонение совокупной факторной производительности (СФП) ЦФО от СФП Российской Федерации.

2. Кривая Филлипса для зарплат:

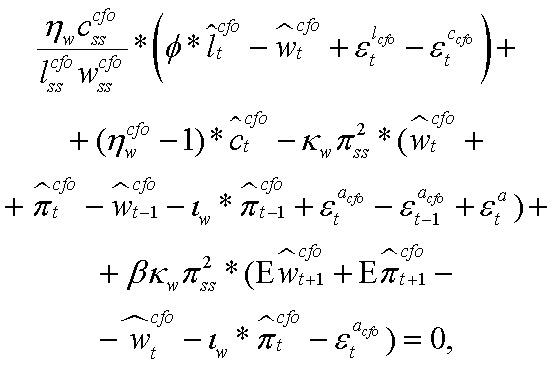
где 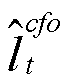 — разрыв совокупного труда ЦФО;  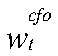— разрыв реальных заработных плат ЦФО;  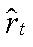— разрыв ставки ЦБ;  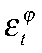— шок СФП Российской Федерации;  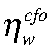— эластичность зарплат;  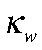— коэффициент издержек подстройки зарплат;  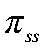— целевое значение инфляции;  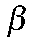— коэффициент межвременного дисконтирования;  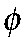— эластичность труда в функции полезности домохозяйств;  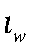— коэффициент жесткости зарплат;  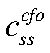— steady-state (устойчивое состояние) потребления ЦФО;  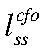— steady-state совокупного труда ЦФО;  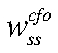— steady-state реальных заработных плат ЦФО.

Инвестиционные производители производят инвестиции в основной капитал, после чего сдают его в аренду фирмам. Каждый инвестиционный производитель максимизирует дисконтированную прибыль при условии уравнения накопления капитала. В итоге получаются следующие уравнения:

1. Уравнение накопления капитала:

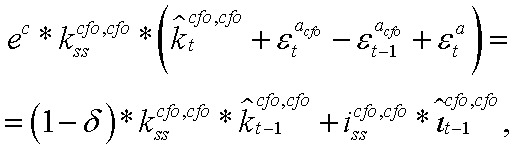
где 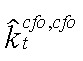 — разрыв капитала ЦФО, сдаваемого в аренду в ЦФО;  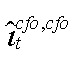— разрыв инвестиций ЦФО в капитал, сдаваемый в аренду в ЦФО;  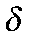— коэффициент амортизации капитала;  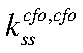— steady-state капитала ЦФО, сдаваемого в аренду в ЦФО;  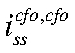— steady-state инвестиций ЦФО в капитал, сдаваемый в аренду в ЦФО;  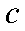— темп сбалансированного роста экономики.

2. Уравнение цены капитала:

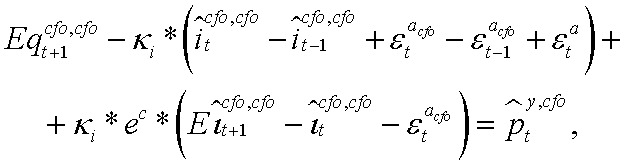
где 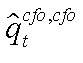 — разрыв цены капитала ЦФО, сдаваемого в аренду в ЦФО;  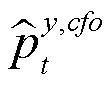— разрыв относительного уровня цен производителей ЦФО;  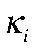— коэффициент издержек подстройки объема инвестиций.

3. Уравнение стоимости аренды капитала:

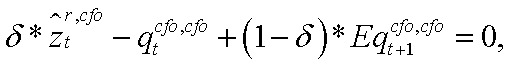
где 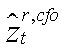 — разрыв относительной стоимости аренды капитала ЦФО.

Еще одним важным агентом в модели являются фирмы, производящие используемое в дальнейшем для потребления домохозяйствами и государством благо. Объемы производимого блага зависят посредством производственной функции Кобба — Дугласа от капитала и труда, которые фирма арендует у соответствующих агрегаторов. Каждая фирма решает задачу максимизации дисконтированной прибыли при условиях предложения труда и капитала. Предполагается, что фирмы несут издержки при изменении цен на уровень, отличающийся от наперед заданного, посредством введения жесткости цен по Ротембергу. После решения оптимизационной задачи для фирм получаются следующие уравнения:

1. Кривая Филлипса для цен производителей:

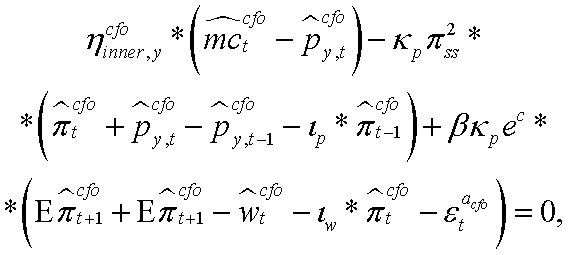
где 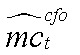 — разрыв предельных издержек производителей ЦФО;  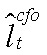— разрыв совокупного труда ЦФО;  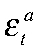— шок совокупной факторной производительности Российской Федерации;  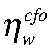— эластичность зарплат;  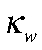— коэффициент издержек подстройки зарплат;  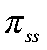— целевое значение инфляции;  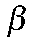— коэффициент межвременного дисконтирования;  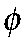— эластичность труда в функции полезности домохозяйств;  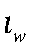— коэффициент жесткости зарплат;  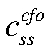— steady-state потребления ЦФО;  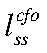— steady-state совокупного труда ЦФО;  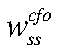— steady-state реальных заработных плат ЦФО.

2. Кривая спроса на труд:

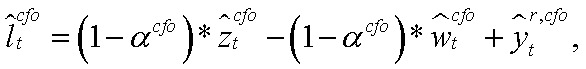
где 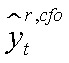 — разрыв произведенного выпуска ЦФО;  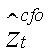— разрыв реальной стоимости аренды капитала ЦФО;  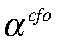— коэффициент при труде в производственной функции Кобба — Дугласа ЦФО.

3. Кривая спроса на капитал:

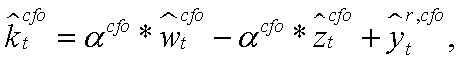
где 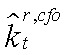 — разрыв капитала, используемого в производстве ЦФО.

В модели присутствует Центральный банк, целью которого является поддержание разрыва совокупной инфляции около нуля путем установки ставки по кредитам для домохозяйств согласно правилу Тейлора:

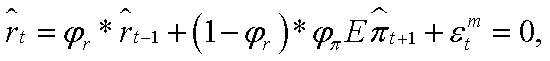
где 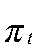 — разрыв инфляции Российской Федерации;  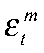— шок монетарной политики;  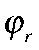— коэффициент инерции ДКП;  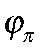— коэффициент реакции ДКП на инфляцию.

Для анализа свойств модели предложено три сценария реакции спроса на изменение ставки Центрального банка в анализируемых регионах. Шок спроса в каждом сценарии задан равным одному стандартному отклонению [4].

Сценарий 1 — положительный шок спроса в ЦФО (рис. 1). В краткосрочном периоде совокупный спрос в ЦФО превышает равновесное значение, что приводит к положительному разрыву выпуска. Это создает повышательное давление на инфляцию в ЦФО. Благодаря эффекту «перетекания» конечного товара (spillover-эффект) инфляционное давление распространяется и на ОРР. В результате инфляция в целом по России ускоряется, что вызывает необходимость повышать номинальную процентную ставку. Меры денежно-кредитного регулирования помогают вернуть макроэкономическое равновесие. При этом в других регионах увеличивается разрыв выпуска, однако данная тенденция здесь менее заметна.

Сценарий 2 — положительный шок государственного спроса в ЦФО (рис. 2); сценарий 3 — положительный шок государственного спроса в ОРР (рис. 3).

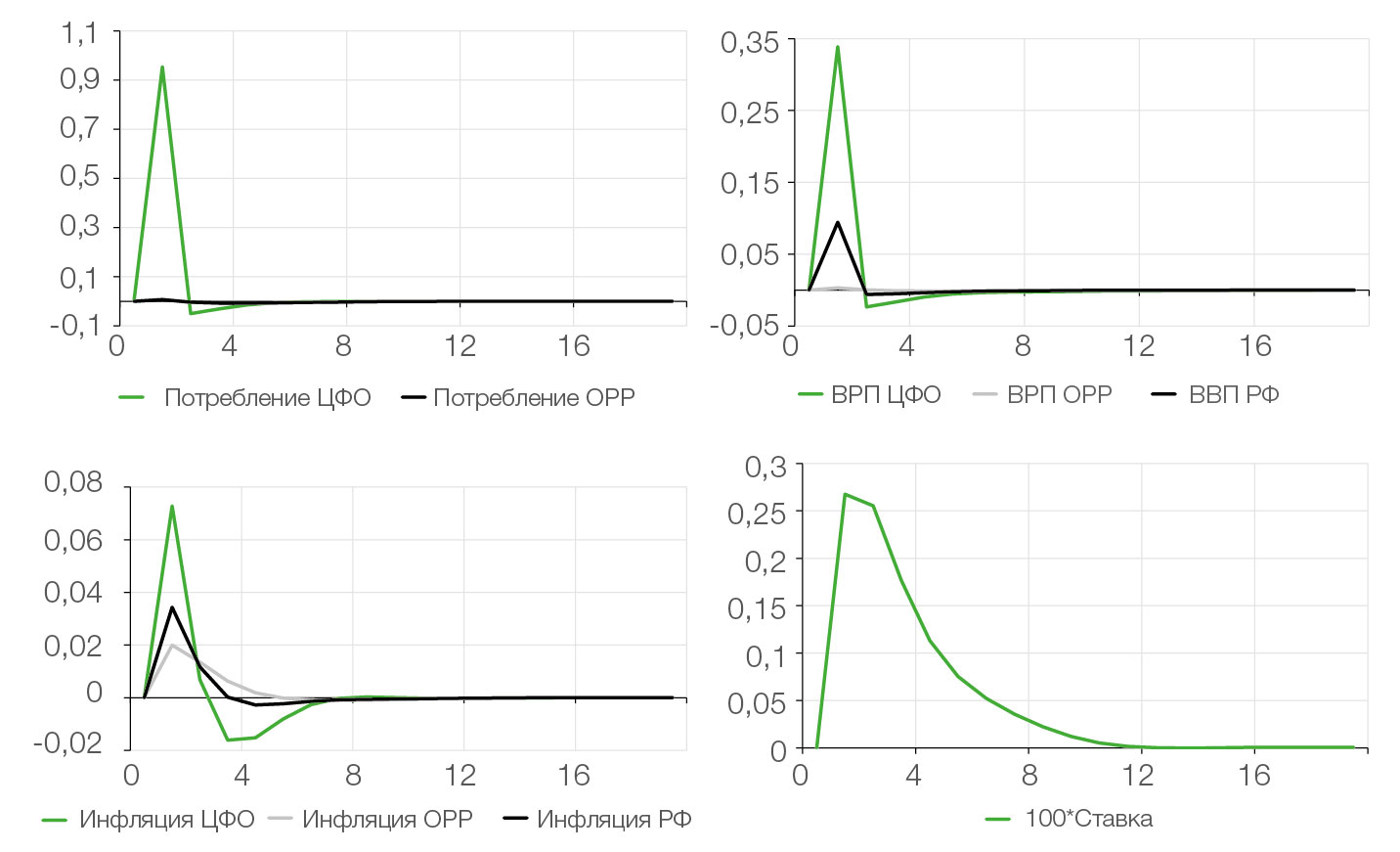
Рис. 1. Сценарий 1: положительный шок спроса в ЦФО (оси абсцисс — кварталы, оси ординат — доли, %)

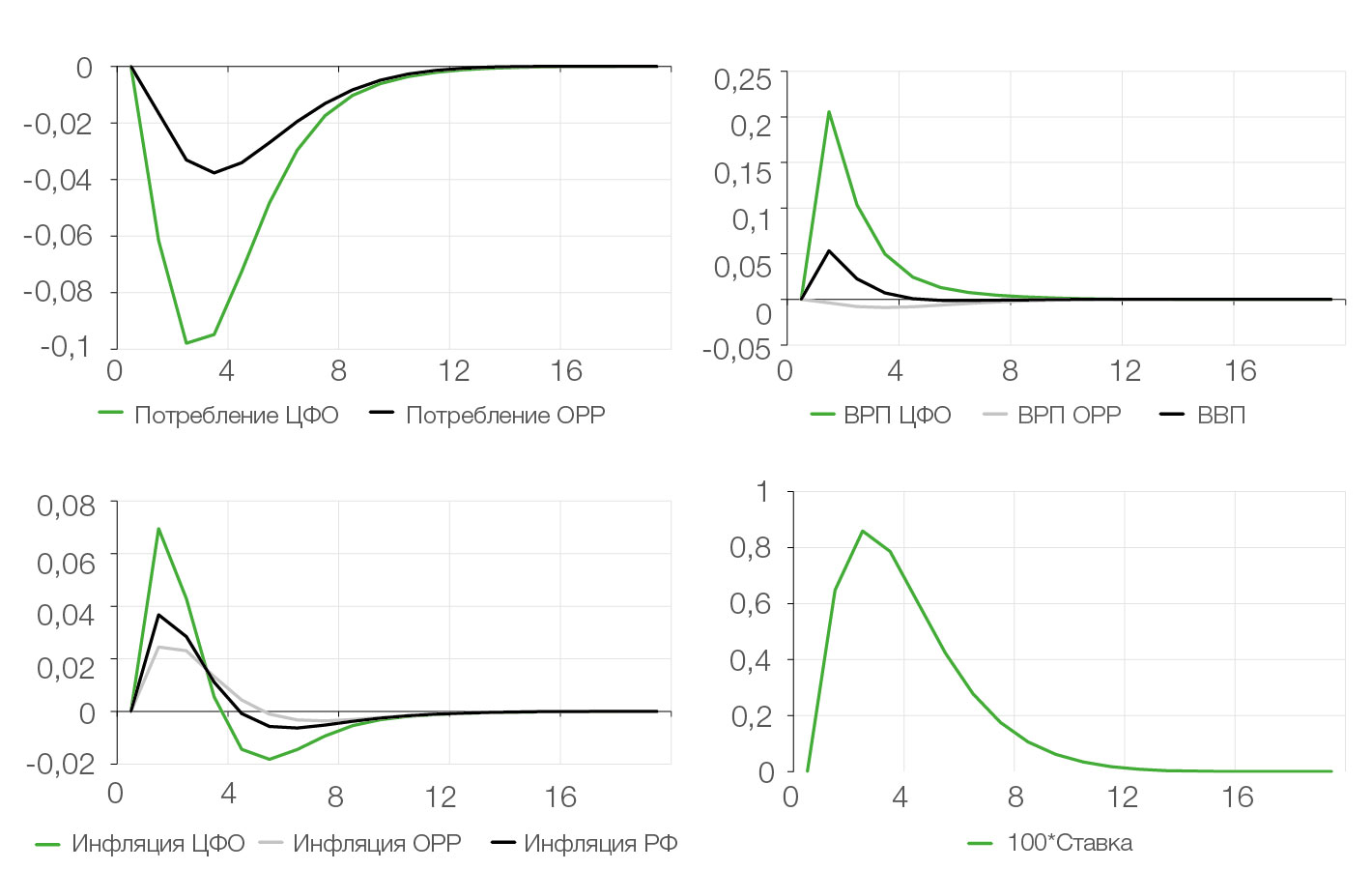
Рис. 2. Сценарий 2: положительный шок государственного спроса в ЦФО (оси абсцисс — кварталы, оси ординат — доли, %)

Рис. 3. Сценарий 3: положительный шок государственного спроса в ОРР (оси абсцисс — кварталы, оси ординат — доли, %)

В краткосрочном периоде совокупный государственный спрос в ЦФО (или ОРР) превышает равновесное значение, что приводит к положительному разрыву выпуска в соответствующем регионе. Это создает повышательное давление на инфляцию в ЦФО (или ОРР), которое благодаря spillover-эффекту передается и на другой регион (ОРР или ЦФО). Рост цен вызывает замедление потребления как в ЦФО (или ОРР), так и в ОРР (или ЦФО), что приводит к формированию отрицательного разрыва выпуска в соседнем регионе. Как и в первом сценарии, ускорение инфляции в целом по России вызывает повышение номинальной процентной ставки со стороны ЦБ, что способствует стабилизации системы.

Стоит отметить различия в реакции экономики на шоки государственного спроса в ЦФО и ОРР. Например, отношение максимальных разрывов потребления в случае шока в ЦФО примерно в два раза превышает аналогичное отношение для шока в ОРР. Это указывает на существенную неоднородность реакции ЦФО и ОРР на изменения бюджетных расходов, что подчеркивает важность учета региональных особенностей при анализе экономической динамики.

Заключение

ДСОЭР-модель представляет собой мощный инструмент для анализа макроэкономических процессов, позволяя учитывать не только разнородные экономические шоки, но и их пространственную неоднородность. Использование таких моделей дает возможность более точно оценивать последствия денежно-кредитной, бюджетной и структурной политики с учетом региональной специфики. Это, в свою очередь, способствует принятию более обоснованных решений, направленных на сглаживание межрегиональных дисбалансов и обес­печение устойчивого экономического роста. Таким образом, дальнейшее развитие и применение ДСОЭР-моделей может существенно повысить качество макроэкономического прогнозирования и политического планирования, особенно в условиях высокой пространственной дифференциации экономических процессов.