Современные подходы к оценке регионального разрыва выпуска

Введение

Концепция потенциального выпуска играет важную роль в проведении денежно-кредитной политики (ДКП): в попытке управлять совокупным спросом через регулирование денежного предложения Центральному банку интересен уровень выпуска, соответствующий долгосрочному (устойчивому) равновесию в экономике.

Потенциальный уровень выпуска (далее — потенциал) является такой же характеристикой устойчивого равновесия, как и нейтральная ставка Банка России, инфляция в окрестности таргета, безработица в окрестности NAIRU и др. Однако даже при относительно низкой инфляции в экономике могут накапливаться дисбалансы, угрожающие финансовой стабильности, которые должны быть учтены при оценке положения экономики относительно устойчивого уровня.

Теоретический анализ

Разрыв выпуска — разница между оценками фактического и потенциального выпуска, выраженная в процентах. Соответственно,

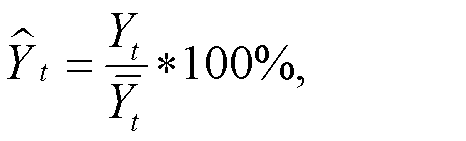
где 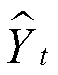 — разрыв выпуска,  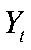— фактический выпуск (ВВП или ВРП для регионов),  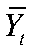— потенциальный выпуск. В логарифмах:

.

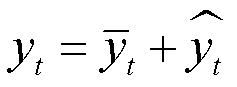Из определения следует, что оценить разрыв озна­чает оценить и потенциал, и наоборот. Разрыв выпуска — мера отклонения фактического выпуска от своей устойчивой траектории — интуитивно понятная категория. Гораздо более спорной и сложной в определении является концепция потенциального выпуска: в зависимости от используемой методологии и школы экономической мысли потенциальный выпуск может быть определен по-разному:

• статистическая оценка тренда фактического выпуска;
• выпуск, достигаемый в ситуации абсолютно гибких цен и зарплат в условиях несовершенной конкуренции (или «эффективный» уровень выпуска, который установился бы в экономике, если бы рынки были эффективными и совершенно конкурентными);
• уровень выпуска, существующий в условиях финансовой стабильности, который экономика способна поддерживать в среднесрочной перспективе, и не вызывающий инфляционное давление в экономике (является такой же характеристикой устойчивого равновесия, как и нейтральная ставка Банка России, инфляция в окрестности таргета, безработица в окрестности NAIRU и др.).

Попытки количественной оценки разрыва выпуска неизбежно сталкиваются с проблемой точности. Во-первых, разрыв выпуска — ненаблюдаемая величина. Во-вторых, фактические ряды (выпуска, населения в трудоспособном возрасте, капитала и др.) — статистическая оценка, полученная Росстатом, также требует уточнения из-за возможного пересмотра данных в будущем, изменений в методологии расчета, статистической погрешности.

Используемая модель играет решающую роль в качестве оценок разрыва. Оценки разных моделей обладают разной дисперсией и размахом доверительных интервалов, к тому же модели, включающие разные показатели, демонстрируют разные результаты, что в общем случае усложняет процесс анализа.

Оценка регионального разрыва выпуска, в свою очередь, усложняется более низким качеством данных: некоторые важные временны́е ряды не доступны вовсе или доступны на низких частотах (например, ВРП по федеральным округам поставляется с годовой частотностью, в то время как ВВП Российской Федерации — с квартальной). Кроме того, неочевидным является вопрос о том, как учитывать spillover-эффекты между регионами: в идеале это требует построения как минимум мультирегиональной модели по аналогии с DSGE-моделью (Dynamic Stochastic General Equilibrium Model) или QPM (Quarterly Projection Model), но в таком случае модель утрачивает простоту интерпретации.

Осознавая сложности с построением качественной оценки разрыва выпуска и невозможность построения сколь угодно точной оценки, логично сконцентрироваться на моделях типа white-box — моделях, основной задачей которых выступает доступная демонстрация взаимосвязей между переменными. В таком фреймворке Дж. Мюррей [5] предлагает использовать два критерия качества оценки разрыва выпуска: стабильность (последние точки не должны сильно изменяться при поступлении новых данных, а сама траектория потенциала не должна быть волатильной) и правдоподобность (нарратив, позволяющий построить оценку потенциала, должен соответствовать действительности и экспертным представлениям).

Среди некоторых исследователей распространена практика взвешенного усреднения оценок разрыва выпуска, полученных с помощью разных моделей, при этом веса устанавливаются экспертно. Это может быть полезно, когда необходима единственная синтезированная оценка разрыва выпуска либо когда несколько альтернативных оценок разрыва сложно коммуницировать.

В литературе распространены все упомянутые выше подходы к получению оценок разрыва выпуска. В качестве отправной точки чаще всего выбирают оценки, полученные фильтром Ход­рика — Прескотта [4]. В статье [1] предприняты попытки использовать DSGE-модели для оценки разрыва выпуска и сделан вывод о том, что подход существенно влияет на интерпретируемость оценок разрыва (потенциала) и плюрализм оценок. В исследовании А. Аличи и соавторов [2] разработан многомерный фильтр на основе данных по США с ключевой особенностью — включением экзогенных оценок steady state в динамику трендовых переменных. Так можно получить более содержательные и интерпретируемые результаты по сравнению с моделями, не учитывающими steady state. Особо популярны среди исследователей модели, основанные на производственной функции. М. Тот [6] строит модель для еврозоны вокруг производственной функции Кобба — Дугласа в духе подхода, предложенного С. Бевериджем и С. Р. Нельсоном в 1981 г., и учитывает важные циклические взаимосвязи, такие как кривая Филлипса и закон Оукена. Ж. Гильошон и Ж. Ле Ру [3] расширяют модель М. Тота [6], добавляя в модель индекс финансовых условий и эксплицитно прописывая динамику факторной производительности.

Статистическая оценка потенциала выпуска ЦФО с помощью HP-фильтра

В качестве отправной точки исследования было решено использовать фильтр Ходрика — Прескотта, так как оценки HP-фильтра могут быть полезны при получении усредненной оценки потенциала. Включение HP-фильтра в расчет помогает «сгладить» траекторию на тех промежутках, где структурные модели дают чересчур дисперсные оценки. Применялась классическая функция потерь:

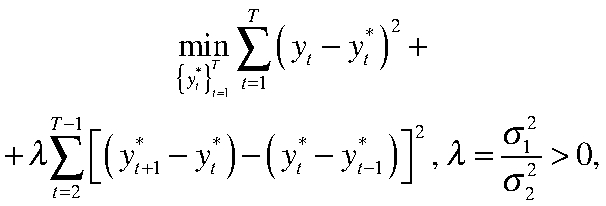
где 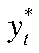 — потенциальный выпуск;  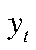— ВРП ЦФО;  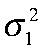— дисперсия ВРП ЦФО;  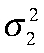— дисперсия потенциального выпуска. При оценке потенциального выпуска в литературе не приводится эвристик для выбора гиперпараметра λ, однако обычно для квартальных данных используют λ = 1600 и λ = 100 — для годовых. Выбор λ во многом определяет поведение фильтра на последних точках выборки. Результаты моделирования представлены на рисунке 1.

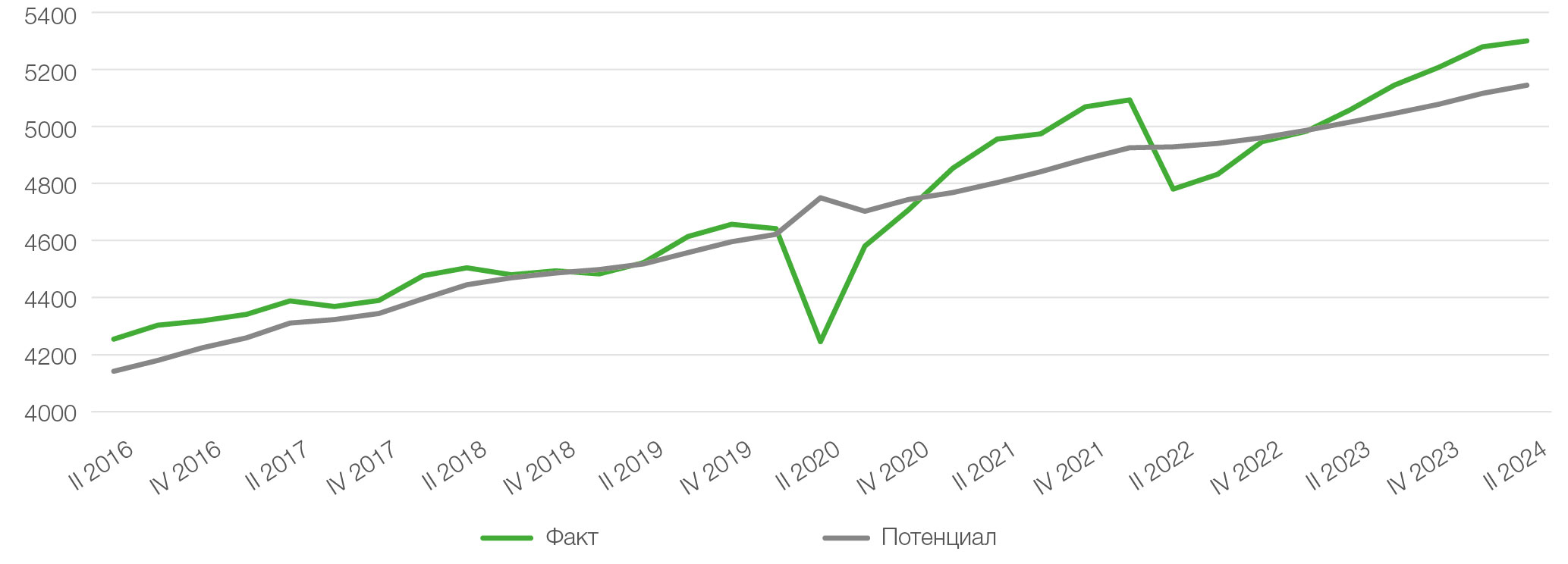
Рис. 1. Оценка потенциала с помощью HP-фильтра, λ = 1600

Одним из недостатков использования фильтра Ход­рика — Прескотта является неинтерпретируемость результатов, однако такая траектория потенциала является хорошей отправной точкой. Во-первых, она соответствует представлениям о персистентности потенциала: траектория идеально гладкая и не склонна к резким изменениям. Во-вторых, результат совпадает с экспертным нарративом по ключевым позициям: здесь наблюдаются и отрицательный разрыв выпуска (во время пандемии COVID-19 и в начале 2022 г.), и перегрев экономики (в 2021 г. и в 2023–2024 гг.).

Оценка разрыва и потенциала выпуска ЦФО с помощью модели ненаблюдаемых компонент

Модель строится вокруг производственной функции Кобба — Дугласа: такой подход позволяет включить значимые для определения потенциала переменные и сохранить экономическую структуру и интерпретируемость модели.

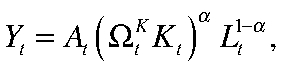
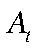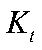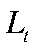где  — общая факторная производительность, и  — капитал и труд соответственно,  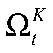— загрузка мощностей. Предполагается, что экономика характеризуется постоянной отдачей от масштаба.

После перехода к натуральным логарифмам:

.

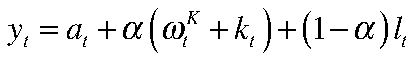Учет финансовых условий позволяет включить в анализ финансовый цикл, который оказался значимым для динамики экономики в целом в период кризиса 2008 г.:

.

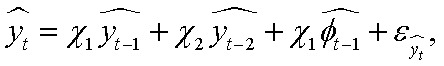
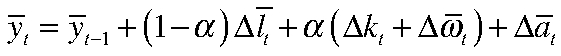В остальном модель является репликацией модели Тота [6].

Мировой кризис 2008 г. показал, что центральные банки должны учитывать финансовые условия как элемент (переменную) бизнес-цикла. Научный консенсус сдвинулся в сторону учета финансовых условий в моделях оценки разрыва выпуска [3].

Индекс финансовых условий рассчитан как главная компонента с наибольшим собственным значением. В качестве данных взяты следующие показатели (все ряды центрированы и нормированы):

• RUONIA, первые разности, Банк России;
• USD/RUB, первые разности, Банк России;
• индикатор бизнес-климата Банка России в ЦФО (баланс ответов по данным мониторинга Банка России);
• изменение спроса на продукцию, товары, услуги в ЦФО (баланс ответов по данным мониторинга Банка России для различных отраслей, в том числе транспортировки и хранения, розничной торговли, за исключением торговли автотранспортными средствами и мотоциклами).

Индекс условий отражает, с одной стороны, жесткость финансовых условий (условия кредитования, внешней торговли), а с другой — ожидания самих предприятий относительно бизнес-климата и спроса на их продукцию. Таким образом, более высокие значения индекса соответствуют более благоприятным условиям для ведения бизнеса.

Индекс условий используется в модели следующим образом:

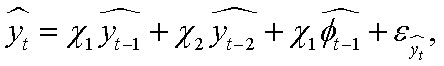
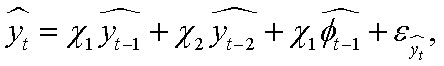
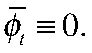
Ненаблюдаемые временны́е ряды, как и параметры модели, оцениваются с помощью фильтра Калмана — рекурсивного алгоритма, который может быть применен к представлению модели в пространстве состояний.

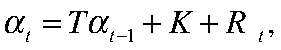
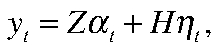
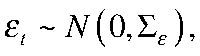
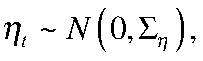
где 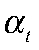 — вектор ненаблюдаемых состояний;  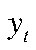— вектор наблюдаемых переменных;  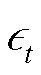— вектор возмущений уравнений состояний, нормально распределенных с нулевой средней и ковариационной матрицей 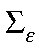;  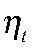— вектор возмущений наблюдаемых переменных с ковариационной матрицей .

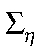Учитывая первоначальные состояния 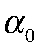, фильтр Калмана обеспечивает оптимальные линейные оценки ненаблюдаемых состояний.

Модель оценивается в два этапа.

1. Применяя теорему Байеса, логарифм апостериорного распределения, 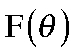, может быть выражен так:

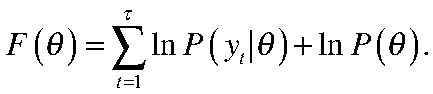
2. Полученные оценки используются как первоначальные в методе максимального правдоподобия:

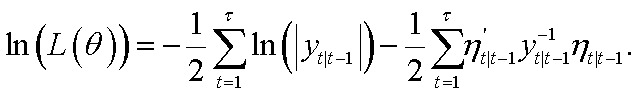
Ковариационные матрицы заполняются эксперт­но. Априорные характеристики (распределение, средняя, дисперсия, интервалы) задаются эксперт­но. Стоит отметить, что ненаблюдаемые переменные могут быть оценены только с высокой долей неопределенности.

Результаты оценки потенциала представлены на рисунке 2.

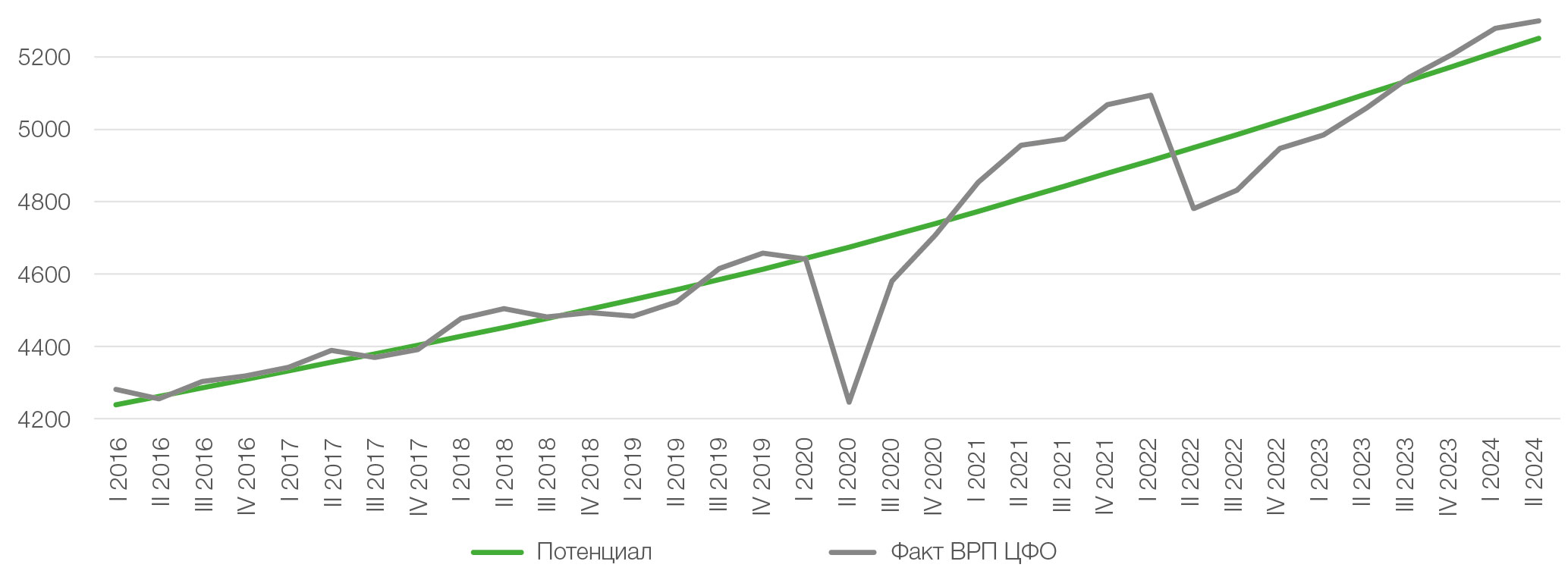
Рис. 2. Оценка потенциала с помощью модели ненаблюдаемых компонент

Результаты и рекомендации

Главным преимуществом оценки разрыва и потенциала полуструктурными моделями является интерпретируемость результатов. Так, UCM позволяет строить декомпозиции разрыва выпуска и роста ВРП:

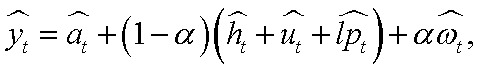
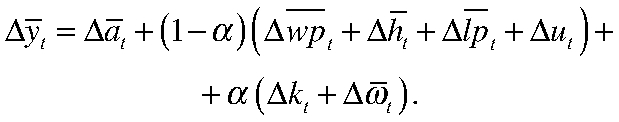
Результаты декомпозиций представлены на рисунках 3 и 4. Перегрев экономики ЦФО в I квартале 2022 г. — II квартале 2024 г. большей частью объясняется факторами рынка труда (рис. 3): стабильно значимый вклад вносят разрыв продолжительности рабочей недели и безработицы. Помимо этого, разрыв увеличивает загрузка производственных мощностей. Остальная динамика разрыва объясняется преимущественно разрывом совокупной факторной производительности.

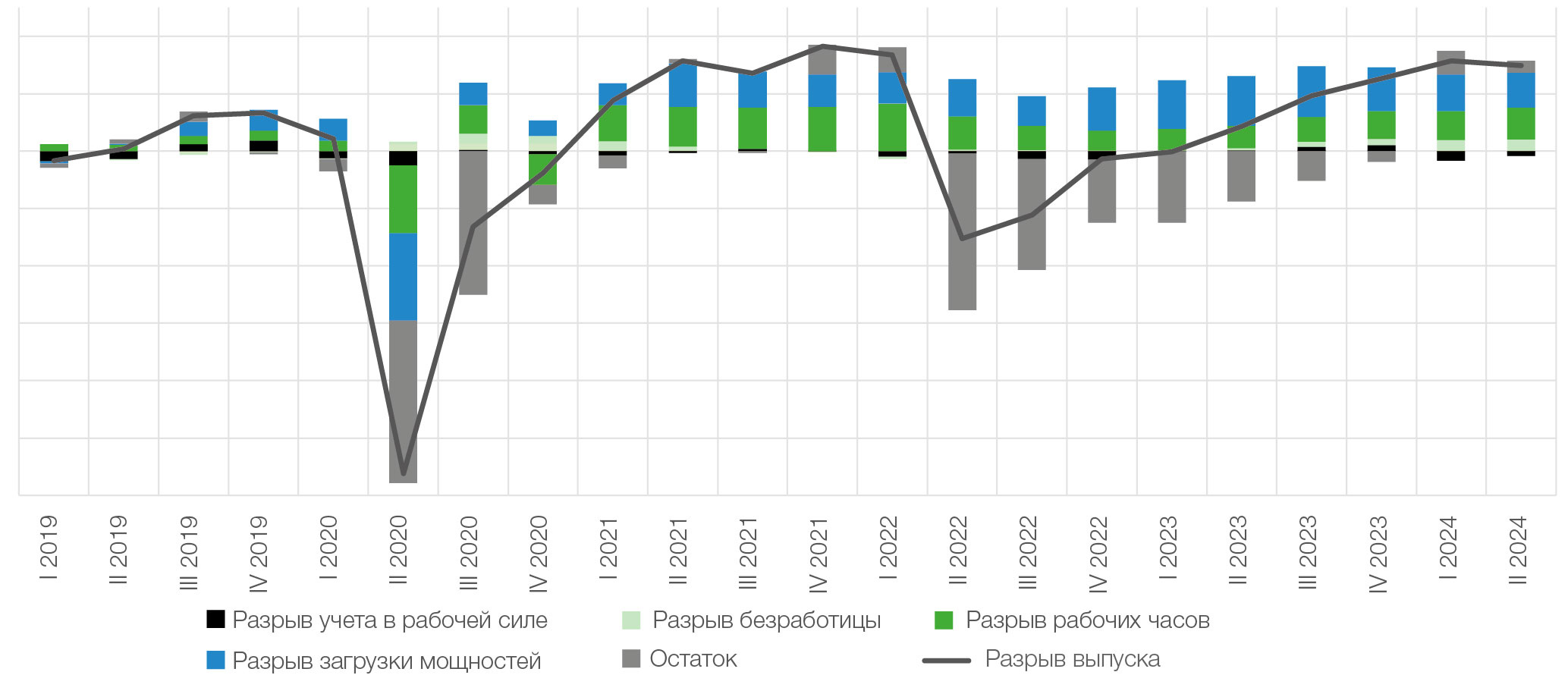
Рис. 3. Декомпозиция разрыва выпуска

Исторически рост ВРП ЦФО во многом объяснялся реализацией инвестиций в основной капитал (рис. 4), однако в 2023 г. рост запаса капитала практически остановился, что может быть связано как с падением отдачи от инвестиций, так и с ограничениями на стороне предложения труда.

Рис. 4. Декомпозиция потенциала выпуска

Таким образом, региональный разрыв выпуска может быть оценен моделями, не учитывающими межрегиональное взаимодействие, причем результаты не будут значимо отличаться от оценок двухрегиональной квартальной прогнозной модели. Особое место в анализе разрыва и потенциала выпуска занимает интерпретируемость результатов: с этой задачей успешно справляются модели ненаблюдаемых компонент, включающие структурные уравнения. Для быстрой оценки потенциала подойдет и фильтр Ходрика — Прескотта: все три оцененные траектории оказываются близкими между собой и позволяют построить похожий нарратив.

Вместе с тем предложенный подход, с использованием индекса условий и базирующийся на производственной функции, позволяет получать интерпретируемые с экономической точки зрения оценки.

Стоит отметить, что оценки потенциала даже в полуструктурных фильтрах подвержены существенному пересмотру. Это еще раз подтверждает неопределенность оценок потенциала и разрыва выпуска.